F1 Parabola与Rectangular Hyperbola考点精讲
Parabola与Rectangular Hyperbola知识点不多,但由于基础数学部分的平面几何只涉及直线与圆相关内容,因此Parabola与Rectangular Hyperbola相关内容对于很多同学而言较新较陌生。需要通过反复练习提高对相关考点的敏感度、提高做题熟练程度。
Parabola与Rectangular Hyperbola在考试中占比不低, 部分同学失分严重。通常会考察1道大题,有时会考2道大题。大部分情况下原始分值在15分左右,可以说分值非常重。如果不能正确完成Parabola与Rectangular Hyperbola相关题目,将会影响F1得A。
本章对于计算要求不高,计算部分多与P1、P2内容结合,重点是理解概念。因此,尽管Parabola与Rectangular Hyperbola部分分值较重,但难度并不高,答题关键在与良好的微分基础与对概念的掌握。
(1)Parabola的表达式与图像
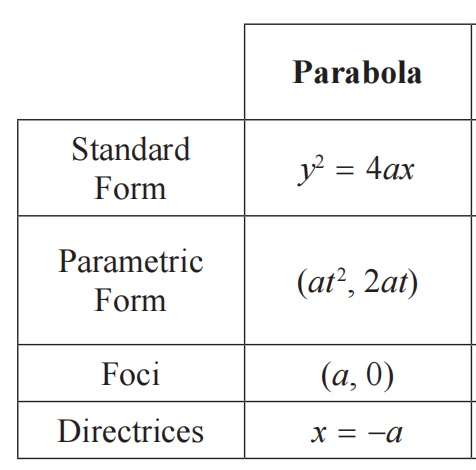
理解Parabola表达式时,一是要理解式中常数a的意义,它与焦点(focus)坐标和准线(directrix)的表达式密切相关;二是要结合参数形式和标准形式(考试时,试题通常会给出参数形式和标准形式的表达式);三是要结合图像理解Parabola的表达式,理解常数a的意义。
结合图像记忆的一个小诀窍是,函数过原点(0 , 0),顶点即原点,a大于0,准线一定在x轴负方向。
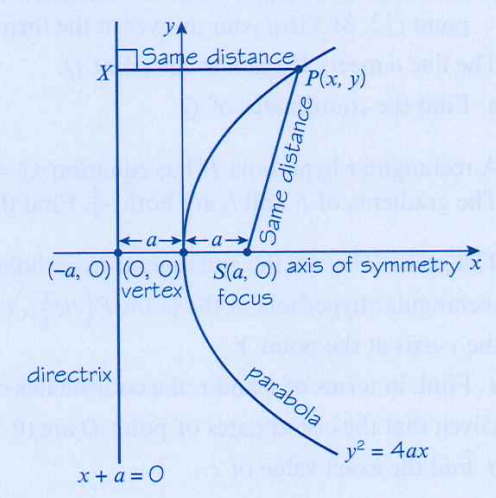
(2)Locus
Parabola是一种locus,这意味着Parabola上所有点都符合一个特定的规则——曲线上每一点到焦点(focus)的距离等于其到准线(directrix)的距离。Parabola的这个性质在2018年考查过:

不记得parabola性质的同学往往在(b)小问上花费不少时间;如果记得性质,可以直接得出SP=PQ=14。
(3)Rectangular Hyperbola的表达式与图像
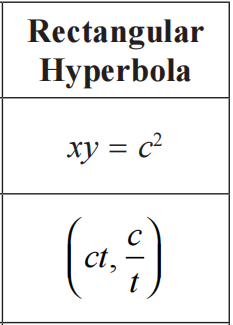
本单元只考察Rectangular Hyperbola的标准表达式和参数表达式,图像基本不考察,主要是结合两个表达式考察求切线、法线、曲线交点等。通常情况下考试会给出两个表达式。
(4)切线tangent和法线normal的计算
考题通常会给出Parabola或Rectangular Hyperbola的两种表达式,求证切线或法线的一般表达式。做对相关题目的关键是把题目给的参数表达的曲线点的坐标当成一个具体的、确定的点来计算。
步骤如下:
①利用标准式求出一阶导,dy/dx;
②根据dy/dx求出切线或法线的斜率;
③利用点斜式求出切线或法线的表达式;
④调整表达式,化简方程。
(5)曲线交点
这部分一般有三种考察方式:
①已知Parabola和Rectangular Hyperbola表达式,求两者交点;
②已知 Parabola或Rectangular Hyperbola其中一个的表达式与某点切线或法线的表达式,已知曲线与直线的一个交点,求另外一个交点;
③已知曲线外一点,求Parabola或Rectangular Hyperbola过该点的切线方程。
前面两种类型利用方程组解等式即可,第③种要利用点斜式和“相切”的条件,计算△=0,求出斜率。
如果你想了解更多A-level课程,留学规划或者有任何疑问,欢迎联系新航道重庆学校。
新航道重庆学校官网:cq.xhd.cn
新航道重庆学校电话:400-185-9090
推荐阅读:
一起来唠唠出国留学英国后的那些“坑”,用自己的血泪教训给大家排个雷~
关于QS排名前100的澳洲院校的花费大全来啦,想去这些学校的小伙伴们有没有准备好钱包呀?